Pilot Maths: 8 Rules of Thumb to Boost Your Flying

Aviation is built on precision. From the moment wheels leave the ground, everything — altitude, heading, fuel burn, descent rate — boils down to maths, formulas, and checklists. There’s no room for guesswork at 5,000 feet. And while there are no true shortcuts in flying, there are tried-and-tested rules of thumb: simple, smart maths tricks that make your cockpit workload lighter and your decisions faster.

These aren’t just clever hacks — they’re mental tools passed down through generations of pilots to help you stay ahead of the aircraft, especially when the workload ramps up. Whether you’re calculating a descent point or estimating crosswind components, these quick rules will keep your flying smooth and safe.

Don't let common pitfalls derail your pilot journey. Discover  9 Flight Training Mistakes to Avoid and stay on track to earning your wings.

Estimating Crosswind Component

The crosswind component is the portion of wind that acts perpendicular to your runway — it's what pushes you sideways during takeoff or landing. Knowing how strong it is helps you decide whether conditions are within your limits (or your aircraft’s).

On the ground, you can check the pilot operating handbooks (POH) or use a flight computer like an E6B. But once you’re in the air, doing trigonometry isn’t exactly practical. Here’s where a rule of thumb becomes your best friend.

Use this quick estimate based on the angle between the wind direction and the runway:

30° off = ~50% of the wind is crosswind

45° off = ~75% of the wind is crosswind

60° or more off = nearly 100% of the wind is crosswind

Example: If the wind is 20 knots and it’s blowing 45° off your runway heading, the crosswind component is about 15 knots — time to check your limits. This simple trick helps you stay sharp in the pattern and make smart go/no-go decisions quickly.

Master the crosswind landings with our comprehensive guide: Taming the Wind: Crosswind Landings Explained. Read more and become a more confident pilot.

10% Weight Increase = 20% Increase in Distance

Weight is one of the most powerful performance factors in aviation — and not in a good way. Heavier aircraft need more lift to get airborne, which means more speed... and more runway. On landing, the increased weight means higher energy to dissipate, longer braking distances, and potentially more wear on brakes and tyres. 

Performance charts in your POH are king, but this rule of thumb gives you a quick estimate before you even open the book: 

A 10% increase in aircraft weight can lead to a ~20% increase in both take-off and landing distance.

Example: Let’s say your aircraft normally takes 1,000 feet to lift off at its standard weight. Now you load up gear and passengers and increase the total weight by 10%. Suddenly, you’re looking at a take-off roll of around 1,200 feet. Same goes for landing — what used to be a 900 ft landing roll could stretch to 1,080 ft.

Note: It’s not linear. Double the weight doesn't just double the distance — it can more than double, depending on density altitude and runway slope.

Enhance your flight training experience with these 14 essential apps. From flight simulators to real-world weather data, these tools will elevate your learning.

Take-off Roll Increases ~10% Per 1,000 ft of Density Altitude

You’ve probably heard it before: “High, hot, or heavy”— three words that make any pilot double-check their take-off numbers. When it comes to performance, density altitude is one of the most critical yet easily overlooked factors.

In simple terms, density altitude is the altitude your aircraft “feels” like it’s at, based on air density. It's a function of pressure altitude corrected for non-standard temperature. 

Higher temperatures = lower air density.  Lower air density = less engine power, less propeller thrust, less wing lift.  In effect, your aircraft behaves as if it’s at a higher altitude — even if you're taking-off at sea level.

For every 1,000 ft increase in density altitude, your take-off roll increases by approximately 10%.

Example: Let’s say you’re flying a light aircraft out of Bristol Airport (Elevation ~622 ft). On a cool spring day at 3°C, the take-off roll is approximately 1,500 ft. However, on a hot summer day with the temperature soaring to 30°C, the density altitude increases significantly, resulting in a take-off roll of about 2,000 ft – roughly 33% longer. 

In short runway scenarios that additional 500 ft on the take-off roll could easily erode your safety margin. During high-elevation operations, the combination of high altitude, heat, and weight can quickly push you to operate at the edge of performance limits. Experiencing sluggish climb rates over rising terrain or in urban environments? Now you understand a key contributing factor.

Airhead Tip: Don’t just check elevation — calculate density altitude before every take-off. Most EFBs or flight planning apps do it automatically, but understanding what it means keeps you sharp.

Do you know the difference between true altitude and pressure altitude? Find out the answer and learn about other types of altitude in our blog: Altitude Basics: 5 Types Of Altitude Explained.

Glide Path Rule

This simple but powerful rule is a handy tool for understanding and visualising descent paths — especially during approach planning or engine-out scenarios. It is rooted in the 60-to-1 concept — a fundamental principle in aviation navigation and descent planning. According to this rule, over 60 nautical miles, a 1° deviation equals 1 NM. That means at a 1° descent angle, you lose about 100 feet per mile.

At a 1° angle of descent, you'll lose approximately 100 feet for every nautical mile flown.

Quick Applications:

• 1° descent = 100 ft/NM

• 3° descent (common glide path) = 300 ft/NM

• If you have 1 NM to lose 600 feet, you'll need a 6° descent angle

Glide path rule helps prevent high approaches by keeping your descent path shallow and manageable. This simple ratio gives pilots a flexible framework to adapt glide angles, descent rates, and visual estimates — especially in non-precision approach situations or emergencies.

Airhead Tip: In emergencies or power-off scenarios, use this to assess if you can reach a safe landing spot. If you’re 10 miles out at 5,000 feet, a 1° descent won’t cut it — but it helps you start gauging.

Consistently achieve smooth landings and master flap adjustments with our in-depth guide,  Flaps, Lift & Drag: The Secret to Smooth Landings.

Distance Needed for Descent

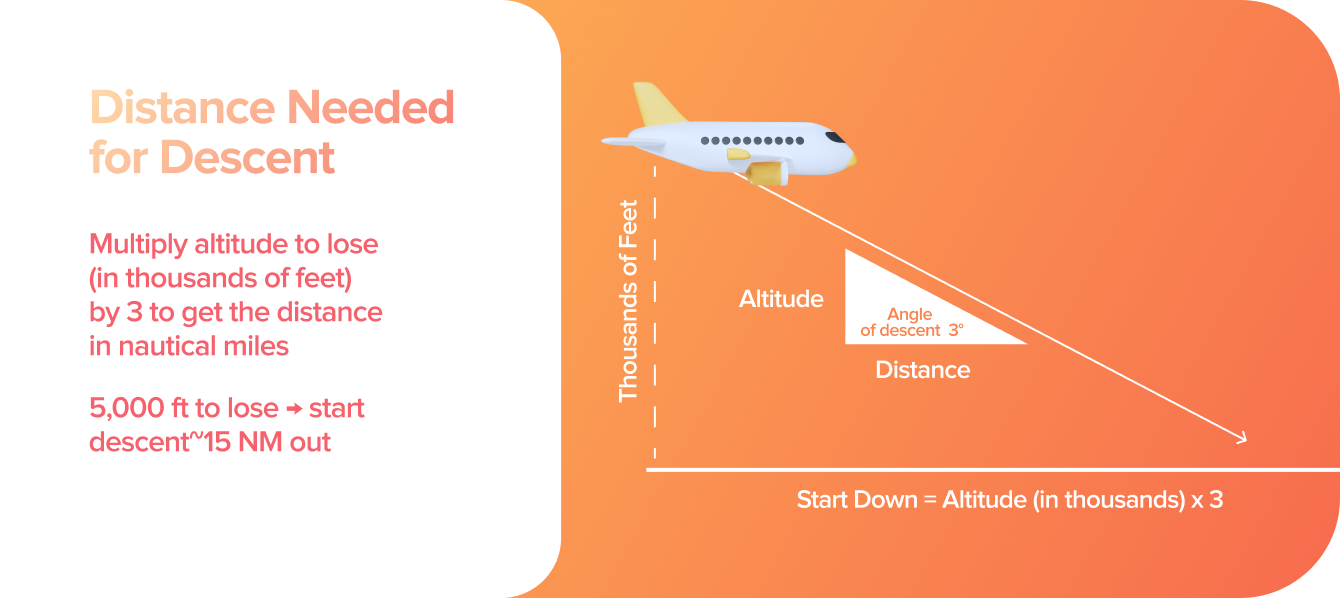
Flying a smooth, consistent descent isn’t just about comfort — it’s about performance, efficiency, and safety. While you might get away with a "chop-and-drop" in a Cessna 172, larger aircraft require something more refined. That’s where the 3-degree descent path comes in.

This descent profile is so standard that Air Traffic Control procedures and ILS approaches are often built around it. Why 3 degrees? It offers a manageable vertical speed, keeps you within approach limitations, and simplifies descent planning with easy maths.

You can estimate when to start your  3° descent using either of these shortcuts:

Altitude to lose (in feet) ÷ 300 = distance to start descent (NM)

Altitude to lose (in thousands) × 3 = distance to start descent (NM)

Example:  Say you're at 11,000 feet, and need to descend to 2,000 feet. That’s a 9,000 ft descent, and using either method: 9,000 ÷ 300 = 30 NM or 9 × 3 = 30 NM. So, you'd want to begin your descent at least 30 nautical miles out from the destination. Ideally, add a buffer of 3–5 NM so you arrive at pattern altitude slightly ahead of the airfield, not over it.

Note: While dividing altitude to lose by 300 gives you an exact descent distance (e.g. 9,000 ÷ 300 = 30 NM), the “×3” rule is an approximation based on a 3° descent angle. Pilots often round up slightly to build in a margin for error. This buffer allows more time to reduce speed, configure the aircraft, and make small corrections. It's not just maths — it's smart airmanship.

Airhead Tip: Remember, your descent gradient = altitude loss (in hundreds of feet) ÷ distance (in NM). For a 3° descent, this works out to about 318 feet per NM — but estimating with “300 ft per mile” keeps it pilot-friendly in the cockpit.

Are you aware of the attitudes that can sabotage your flying? Discover 5 risky mindsets every pilot should check.

Approach Descent Rate

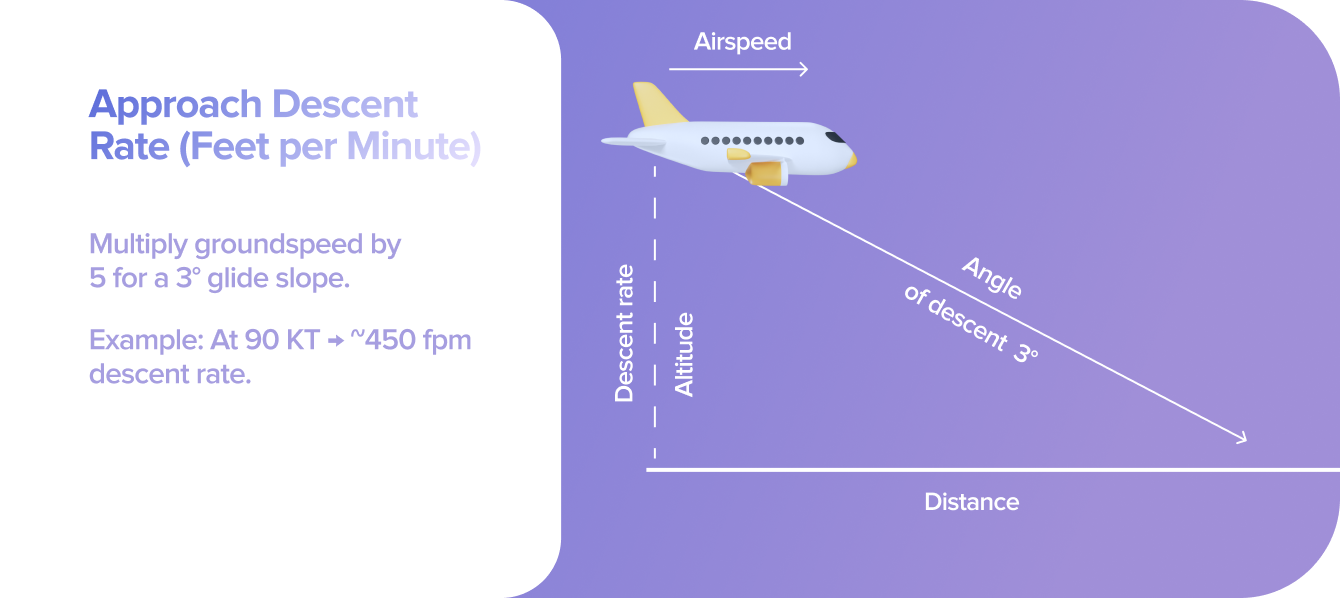
When flying an approach, especially on a 3° glide slope like an ILS, knowing your descent rate in feet per minute (fpm) helps you stay stable and ahead of the aircraft.

Here’s the simple rule:

Multiply your groundspeed by 5 to get your target descent rate for a 3° glide path.

Example: Groundspeed: 90 knots. 90 × 5 = 450 fpm.  So you’ll want to descend at roughly 450 feet per minute to maintain that 3° slope.

This rule gives you a reliable way to quickly calculate how fast you need to descend to stay on that path — no complex maths or charts needed.

Sharpen your judgment in the cockpit. Decision-Making: 8 Key Scenarios for Pilots explores critical situations and provides valuable insights to help you make sound choices under pressure.

Climb Gradient Quick Check

Not every departure gives you miles of flat terrain. Some have trees, hills, antennas — or all three. Whether you're flying IFR or just aiming for solid airmanship, understanding and planning for the right climb gradient ensures you’re not just climbing — but climbing safely. 

Climb gradient is the vertical distance you must climb over a given horizontal distance — typically expressed in feet per nautical mile (ft/NM).  The standard minimum IFR climb gradient is 200 ft/NM. That means for every mile you fly forward, you must climb at least 200 feet to ensure obstacle clearance, terrain avoidance, and safe separation. 

This is where a quick climb gradient check becomes essential. This rule is especially handy when reviewing departure procedures or quickly determining if your aircraft can safely clear terrain, no calculator required.

Multiply your groundspeed by 3.3 to find the required feet-per-minute (fpm) climb rate to meet a 200 ft/NM climb gradient.

Example:  If you're flying at 90 knots groundspeed, you’ll need:  90 × 3.3 = ~300 fpm to stay within required climb parameters.

Why multiply by 3.3? This number comes from converting nautical miles per hour (i.e. groundspeed in knots) to feet per minute.  

Here’s the logic: At 60 knots groundspeed, you travel 1 NM per minute. So, to climb 200 ft/NM, you need a 200 fpm climb rate. As groundspeed increases, your horizontal distance increases, but your climb must keep up.  That’s where 3.3 comes in: it converts your groundspeed in knots to a required climb rate in feet per minute, using a standardised 200 ft/NM gradient. 

Understand the Best Rate of Climb speed. Read our blog post: It's All Connected: TWR, Drag, and the Climb Rates.

Fuel Burn Estimation

While POH numbers are your best source for accurate planning, this simple rule helps you estimate fuel consumption quickly. It’s especially handy for student pilots still getting used to performance charts or when planning a quick cross-country. It’s also a great backup estimate if your E6B’s batteries die or you’re flying an unfamiliar piston aircraft.

1Most piston aircraft burn approximately 0.5 gallons of fuel per cylinder per hour in cruise.

Here are a few examples:

• Cessna 152 (O-235, 4-cylinder) 4 × 0.5 = ~2 gallons/hour

• Cessna 172 (O-320 or O-360, 4-cylinder) 4 × 0.5 = ~2 gallons/hour (real-world cruise: closer to 7–9 GPH due to higher power settings and mixture settings)

• Piper Arrow (O-360, 4-cylinder) 4 × 0.5 = ~2 gallons/hour (again, expect around 9 GPH in cruise)

Remember: This rule works best for leaned cruise power settings (not for climb or full-power ops). Always round up slightly to stay on the safe side of fuel reserves.

Airhead's Takeaway 

These pilot rules of thumb won’t replace your POH or flight planning tools. But they’ll keep you sharp, efficient, and safer in the cockpit.  Train smart, fly safe, and remember: great pilots don’t just know their numbers — they use them.

Quick Reference: 8 Pilot Rules of Thumb